
When a folded band edge with inner radius zero is formed to a hem in a roll forming machine, the material´s spring back causes a considerable problem. The desired cross-section requires that the sheet surfaces should touch closely and should not spring up.
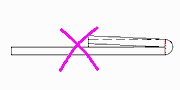
If the fold is roll formed until the sheet surfaces touch, the spring back of the material causes the fold to spring up. This is not the desired result.
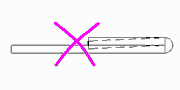
Usually a bending zone is overbent in order to compensate the spring back. If this is tried with the 180 degree bend, the sheet would penetrate itself. This is not possible.
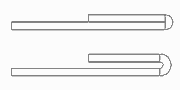
In the previous pass, the fold is opened to a small inner radius by keeping the angle of 180 degree. Because the developed length of the arc increases by this operation, the adjoining line segments have to be decreased by half of the arc lengthening each in order to keep constant the whole sheet width. Afterwards the new arc is developed as usual to the flat sheet (in design direction, i.e. against the sheet running direction). In sheet running direction's view, an open fold is roll formed first. Then it is compressed by a roll pair.
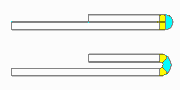
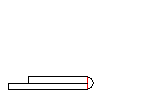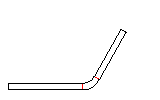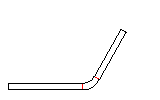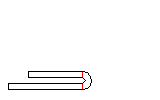
Imagine, the new arc (with the larger inner radius) consists of three parts. The center part has exactly the developed length of the final 180 degree bend with inner radius zero. The two small parts have the developed length, that is subtracted from the adjoining line segments. When the fold is compressed this happens: the large arc is bent down (to inner radius zero) and springs up after leaving the roll forming stand. The two small arcs, however, are bent up (to flat sheet) and spring back to the closed state. So the spring back of the small arcs have an effect in the opposite direction to the spring back of the large arc. By choosing the correct inner radius it is possible that the sum of all spring forces is zero and the 180 degree fold keeps closed. In practice, an inner radius in the range 0.4-0.8 x sheet thickness is used. A larger inner radius gives more effect on the small arcs and creates a permanent force that holds the fold closed.
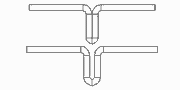
Any arc angle is possible. So the function also can be used e.g. if a symmetrical profile starts with a 90 degree arc.